Buongiorno, chiedo un veloce chiarimento riguardante la slide 29/30 del blocco sulla semantica, dove si prova che se un frame è transitivo allora vale l’assioma “boxp entails boxboxp”.
Non mi è chiara la conclusione che il mondo k porti a boxp dal fatto che j e k portano a p. Sarebbe chiaro se il frame fosse anche riflessivo, e cioè che k si riflettesse su se stesso. Così, avendo transitività e riflessività avremmo un preordine, che infatti è il frame adeguato, come si dice nella slide 18/30, per il sistema s4, caratterizzato per l’appunto dall’assioma “boxp entails boxboxp”. Mancando la transitività però mi riesce difficile capire quel passaggio.
Grazie!
L’idea è questa. Supponiamo . Dobbiamo dimostrare . Supponiamo che è sufficiente dimostrare che . Se è un punto arbitrario tale che allora per transitività. Ora, per ipotesi . Dunque . Ma poiché era uno stato arbitrario in relazione con otteniamo che , come desiderato.
Buongiorno, chiedo un veloce chiarimento riguardante la slide 29/30 del blocco sulla semantica, dove si prova che se un frame è transitivo allora vale l’assioma “boxp entails boxboxp”.
Non mi è chiara la conclusione che il mondo k porti a boxp dal fatto che j e k portano a p. Sarebbe chiaro se il frame fosse anche riflessivo, e cioè che k si riflettesse su se stesso. Così, avendo transitività e riflessività avremmo un preordine, che infatti è il frame adeguato, come si dice nella slide 18/30, per il sistema s4, caratterizzato per l’appunto dall’assioma “boxp entails boxboxp”. Mancando la transitività però mi riesce difficile capire quel passaggio.
Grazie!
L’idea è questa. Supponiamo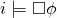 . Dobbiamo dimostrare
. Dobbiamo dimostrare  . Supponiamo che
. Supponiamo che 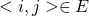 è sufficiente dimostrare che
è sufficiente dimostrare che 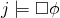 . Se
. Se 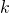 è un punto arbitrario tale che
è un punto arbitrario tale che 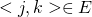 allora
allora 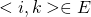 per transitività. Ora, per ipotesi
per transitività. Ora, per ipotesi 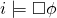 . Dunque
. Dunque 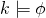 . Ma poiché
. Ma poiché 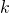 era uno stato arbitrario in relazione con
era uno stato arbitrario in relazione con 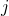 otteniamo che
otteniamo che 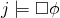 , come desiderato.
, come desiderato.