Dimostriamo che per ogni terna di insiemi A,B,C abbiamo:
![]() .
.
Useremo frequentemente che se ![]() allora
allora ![]() qualsiasi sia B. Dimostriamo le due implicazioni separatamente:
qualsiasi sia B. Dimostriamo le due implicazioni separatamente:
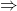 dimostriamo per assurdo, cioè dimostriamo che se
dimostriamo per assurdo, cioè dimostriamo che se 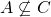 allora
allora 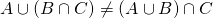 . Sia
. Sia 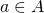 ma
ma 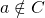 . Allora
. Allora 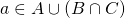 ma non sta in
ma non sta in 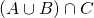 perché non sta in C.
perché non sta in C.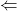 Sia quindi
Sia quindi 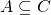 e dimostriamo
e dimostriamo 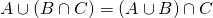 , quindi dobbiamo dimostrare le due inclusioni
, quindi dobbiamo dimostrare le due inclusioni
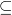 sia
sia 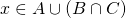 , quindi
, quindi 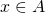 oppure
oppure 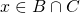 . Nel primo caso
. Nel primo caso 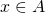 e quindi
e quindi 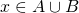 e per ipotesi
e per ipotesi 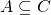 e quindi
e quindi 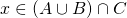 ; nel secondo caso
; nel secondo caso 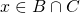 quindi
quindi 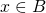 e
e 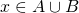 e sta già in C quindi
e sta già in C quindi 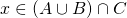 .
.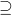 sia
sia 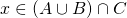 , allora
, allora 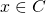 e forse
e forse 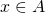 oppure
oppure 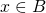 . Se
. Se 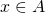 , allora sicuramente
, allora sicuramente 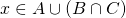 ; ma se
; ma se 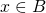 e quindi
e quindi 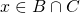 e quindi in
e quindi in 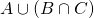 .
.
Una delle inclusioni vale incondizionatamente? Commenti? Correzioni? Chiarimenti?