Seconda lezione: la differenza simmetrica è associativa

Proviamo che per tre sottoinsiemi $S,T,V$ di un insieme X la differenza simmetrica $S\Delta T=(S\setminus T)\cup (T\setminus S)$ è associativa, cioè $(S\Delta T)\Delta V=S\Delta(T\Delta V)$ .

Ogni elemento dell’insieme ambiente può stare o no dentro questi insiemi e quindi abbiamo 8 possibilità:

elemento sta in	S	T	V
1	Sì	Sì	Sì
2	Sì	Sì	No
3	Sì	No	Sì
4	No	Sì	Sì
5	Sì	No	No
6	No	Sì	No
7	No	No	Sì
8	No	No	No

Ricordiamo che un elemento sta in $A\Delta B$ se nella tabella abbiamo (Sì,No) oppure (No,Sì) ma non appartiene quando abbiamo (Sì,Sì) o (No,No). Ora mostriamo che i due insiemi $(S\Delta T)\Delta V$ e $S\Delta (T\Delta V)$ sono uguali controllando in tutti i casi:

non sta in 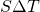$S\Delta T$ ma sta in V quindi sta in 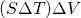$(S\Delta T)\Delta V$ , e non sta in 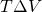$T\Delta V$ ma sta in S quindi sta in $S\Delta (T\Delta V)$ .
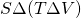non sta in 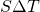$S\Delta T$ nè in V quindi non sta in 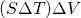$(S\Delta T)\Delta V$ , sta in 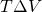$T\Delta V$ e in S quindi non sta in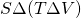 $S\Delta (T\Delta V)$
vedi 2
vedi 2
sta in 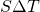$S\Delta T$ ma non in V quindi sta in 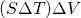$(S\Delta T)\Delta V$ , non sta in 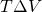$T\Delta V$ ma sta in S quindi sta in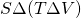 $S\Delta (T\Delta V)$
vedi 5
vedi 5
tutti no quindi non sta in entrambi gli insiemi

Quindi ogni elemento di X deve soddisfare uno degli 8 casi di sopra, e in ciascuno dei casi i due insiemi sono uguali quindi ho dimostrato che sono uguali come sottoinsiemi di X.

Lascia un commento